soil Bearing Capacity and Calculation of Bearing Capacity

What is bearing capacity of Soil?

The bearing capacity of soil is defined as the capacity of the soil to bear the loads coming from the foundation. The pressure which the soil can easily withstand against load is called allowable bearing pressure.

Following are some types of bearing capacity of soil:

Ultimate bearing capacity of soil (qu)

The gross pressure at the base of the foundation at which soil fails is called ultimate bearing capacity.

Net ultimate bearing capacity (qnu)

By neglecting the overburden pressure from ultimate bearing capacity we will get net ultimate bearing capacity.

Where 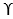= unit weight of soil, Df = depth of foundation

Net safe bearing capacity of soil (qns)

By considering only shear failure, net ultimate bearing capacity is divided by certain factor of safety will give the net safe bearing capacity.

qns = qnu/ F

Where F = factor of safety = 3 (usual value)

Gross safe bearing capacity (qs)

When ultimate bearing capacity is divided by factor of safety it will give gross safe bearing capacity.

qs = qu/F

Net safe settlement pressure (qnp)

The pressure with which the soil can carry without exceeding the allowable settlement is called net safe settlement pressure.

Net allowable bearing pressure (qna)

This is the pressure we can used for the design of foundations. This is equal to net safe bearing pressure if qnp > qns. In the reverse case it is equal to net safe settlement pressure.

How to Calculate Bearing Capacity of Soil?

Calculation of bearing capacity of soil:

For the calculation of bearing capacity of soil, there are so many theories. But all the theories are superseded by Terzaghi’s bearing capacity theory.

Terzaghi’s bearing capacity theory

Terzaghi’s bearing capacity theory is useful to determine the bearing capacity of soils under a strip footing. This theory is only applicable to shallow foundations. He considered some assumptions which are as follows.

1. The base of the strip footing is rough.
2. The depth of footing is less than or equal to its breadth i.e., shallow footing.
3. He neglected the shear strength of soil above the base of footing and replaced it with uniform surcharge. ( 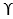Df)
4. The load acting on the footing is uniformly distributed and is acting in vertical direction.
5. He assumed that the length of the footing is infinite.
6. He considered Mohr-coulomb equation as a governing factor for the shear strength of soil.

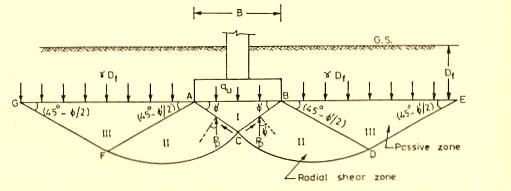
As shown in above figure, AB is base of the footing. He divided the shear zones into 3 categories. Zone -1 (ABC) which is under the base is acts as if it were a part of the footing itself. Zone -2 (CAF and CBD) acts as radial shear zones which is bear by the sloping edges AC and BC. Zone -3 (AFG and BDE) is named as Rankine’s passive zones which are taking surcharge (y Df) coming from its top layer of soil.

From the equation of equilibrium,

Downward forces = upward forces

Load from footing x weight of wedge = passive pressure + cohesion x CB sin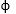

Where Pp = resultant passive pressure = (Pp)y + (Pp)c + (Pp)q

(Pp)y is derived by considering weight of wedge BCDE and by making cohesion and surcharge zero.

(Pp)c is derived by considering cohesion and by neglecting weight and surcharge.

(Pp)q is derived by considering surcharge and by neglecting weight and cohesion.

Therefore,

By substituting,

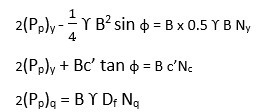
So, finally we get qu = c’Nc + y Df Nq + 0.5 y B Ny

The above equation is called as Terzaghi’s bearing capacity equation. Where qu is the ultimate bearing capacity and Nc, Nq, Ny are the Terzaghi’s bearing capacity factors. These dimensionless factors are dependents of angle of shearing resistance ().

Equations to find the bearing capacity factors are:

Where

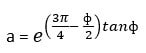
Kp = coefficient of passive earth pressure.

For different values of 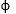, bearing capacity factors under general shear failure are arranged in the below table.

	Nc	Nq	Ny
0	5.7	1	0
5	7.3	1.6	0.5
10	9.6	2.7	1.2
15	12.9	4.4	2.5
20	17.7	7.4	5
25	25.1	12.7	9.7
30	37.2	22.5	19.7
35	57.8	41.4	42.4
40	95.7	81.3	100.4
45	172.3	173.3	297.5
50	347.5	415.1	1153.2

Finally, to determine bearing capacity under strip footing we can use

qu = c’Nc + 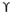Df Nq + 0.5  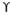B Ny

By the modification of above equation, equations for square and circular footings are also given and they are.

For square footing

qu = 1.2 c’Nc + 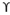 Df Nq + 0.4  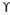B Ny

For circular footing

qu = 1.2 c’Nc +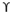Df Nq + 0.3 B Ny

Hansen’s bearing capacity theory

For cohesive soils, Values obtained by Terzaghi’s bearing capacity theory are more than the experimental values. But however it is showing same values for cohesion less soils. So Hansen modified the equation by considering shape, depth and inclination factors.

According to Hansen’s

qu = c’Nc Sc dc ic +  Df Nq Sq dq iq + 0.5  B Ny Sy dy iy

Where Nc, Nq, Ny = Hansen’s bearing capacity factors

Sc, Sq, Sy = shape factors

dc, dq, dy = depth factors

ic, iq, iy = inclination factors

Bearing capacity factors are calculated by following equations.

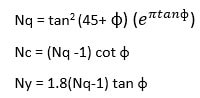
For different values of 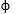 Hansen bearing capacity factors are calculated in the below table.

	Nc	Nq	Ny
0	5.14	1	0
5	6.48	1.57	0.09
10	8.34	2.47	0.09
15	10.97	3.94	1.42
20	14.83	6.4	3.54
25	20.72	10.66	8.11
30	30.14	18.40	18.08
35	46.13	33.29	40.69
40	75.32	64.18	95.41
45	133.89	134.85	240.85
50	266.89	318.96	681.84

Shape factors for different shapes of footing are given in below table.

Shape of footing	Sc	Sq	Sy
Continuous	1	1	1
Rectangular	1+0.2B/L	1+0.2B/L	1-0.4B/L
Square	1.3	1.2	0.8
Circular	1.3	1.2	0.6

Depth factors are considered according to the following table.

Depth factors	Values
dc	1+0.35(D/B)
dq	1+0.35(D/B)
dy	1.0

Similarly inclination factors are considered from below table.

Inclination factors	Values
ic	1 – [H/(2 c B L)]
iq	1 – 1.5 (H/V)
iy	(iq)2

Where H = horizontal component of inclined load

B = width of footing

L = length of footing.